Application of shifted Vieta-Lucas polynomials for the numerical treatment of Volterra-integro differential equations

IKECHUKWU  OTAIDE; Matthew Oluwayemi; KENNETH   OGEH

doi:10.61298/pnspsc.2024.1.84

Authors

Ikechukwu Jackson Otaide Department of Mathematics, Federal University of Petroleum Resources, Effurun, Delta State, Nigeria https://orcid.org/0000-0003-0720-3399
Matthew Olanrewaju Oluwayemi
oluwayemimatthew@gmail.com
Department of Mathematics and Statistics, Margaret Lawrence University, Galilee, Delta State, Nigeria https://orcid.org/0000-0003-3170-6818
Kenneth Oke Ogeh Department of Mathematical Sciences, Edwin Clark University, Kiagbodo, Delta State, Nigeria https://orcid.org/0000-0001-9390-986X

Keywords:

Variational iteration method, Volterra integro differential equation, shifted Vieta-Lucas polynomials

Abstract

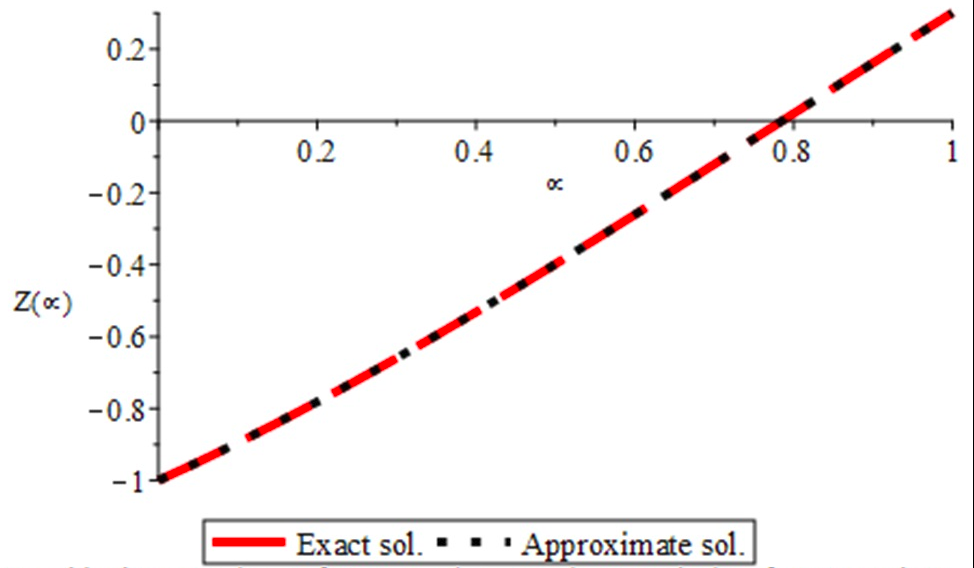
In this study, the numerical solution of the Volterra-integro differential equations was obtained by applying the variational iteration strategy with the shifted Vieta-Lucas polynomials. The proposed method builds the shifted Vieta-Lucas polynomials for the Volterra-integro differential equation which are then used as basis functions for the approximation. Numerical examples were given to establish the effectiveness and dependability of the recommended approach. Calculations were performed using Maple 2022 software.

Dimensions

REFERENCES

R. J. Durrheim & G. R. J. Cooper, “EULDEP: a program for the Euler deconvolution of magnetic and gravity data”, Comput. Geosciences 24 (1998) 545e550. https://www.researchgate.net/publication/30509084.

O. Saheed & Y. Magaji, “Analysis of high-resolution aeromagnetic data over parts of Sokoto basin, North-West Nigeria”, A Journal of Engineering 4 (2022) 14. https://doi.org/10.61762/pajevol4iss2art8601.

C. C. Ku & J. A. Sharp, “Werner Deconvolution for Automatic Magnetic Interpretation and Its Refinement Using Marquardt’s Inverse Modelling”, Geophysics 48 (1983) 754. https://library.seg.org/doi/abs/10.1190/1.1441505.

H. I. E. Hassanein & K. S. Soliman, “Aeromagnetic data interpretation of wadi hawashiya area for identifying surface and subsurface structures, north eastern desert”, Earth Sci. 20 (2009) 117e139. https://www.academia.edu/65050513.

A. Vasanthi, K.K. Sharma & K. Mallick, “On new standards for reducing gravity data, the North American Gravity Database”, Geophysics 71 (2006) 31e32. https://pubs.usgs.gov/publication/70029532.

M. A. Al-Garni, “Geophysical investigation for groundwater in a complex surface terrain, wadi fatima. KSA: A case history. Jordan. J. Civ.”, 3 (2009) 118e136. https://www.researchgate.net/publication/320434111.

G. C. Onyedim & O. O. Ocan, “Spatial periodicities of structural features of the basement complex of southwestern Nigeria deduced from auto-covariance and power spectra of aeromagnetic data. The pacific journal of science and Technology”, Pac. Sci. Technol. 1 (2009) 556e566. https://www.academia.edu/30688857.

R. Mudashir, “Morphometric analysis of Asa and Oyun river basins, North Central Nigeria using geographical information system”, American Journal of Civil Engineering 5 (2007) 379. https://library/doi/j.ajce/10.11648/20170506.20.

M. O. Oyawoye, “The basement complex of Nigeria”, in African geology, T. F. J. Dessauvagie & A. J. Whiteman (Ed), Ibadan University Press, Ibadan, 1972. pp. 66–102. https://www.scirp.org/1160510.

M. A. Rahaman, “Recent advances in the study of the Basement Complex of Nigeria”, in Precambrian geology of Nigeria, geological survey of Nigeria, Kaduna, 1988, pp. 11-43. https://www.scirp.org/1425164.

M. A. Rahaman, “Review of basement geology of southwestern Nigeria”, in Geology of Nigeria, C. A. Kogbe (Ed.), Rock View Nigeria Ltd., Jos, 1989, pp. 39-56. https://www.ijrdo.org/as/article/3817/2857.

P. O. Oluyide, C. S. Nwajide & A. O. Oni, “The geology of Ilorin area”, Bulletin Geological Survey of Nigeria” 42 (1988) 60. https://www.ajol.info/aujst/article/265487/250533.

W. J. Hinze, “The Role of Gravity and Magnetic Methods in Engineering and Environmental Studies”, in Investigations in Geophysics, Geotechnical and Environmental Geophysics: Volume I, Review and Tutorial, 1990, pp. 75. https://doi.org/10.1190/1.9781560802785.ch4.

R. O. Hansen & M. Simmonds, “Multiple source Werner deconvolution”, Geophysics 58 (1993) 1792. https://link.springer.com/article/10.1007/BF00876477.

S. Jain, “An automatic method of direct interpretation of magnetic profiles”, Geophysics 41 (1976) 531. https://doi.org/10.1190/1.1440631.

J. U. Megwara & E.E Udensi, “Structural analysis using aeromagnetic data: case study of parts of southern Bida basin, Nigeria and the surrounding basement rocks”, Earth Sci. Res. 3 (2014) 27. https://www.ccsenet.org/journal//32743.

A. B. Reid, J. M. Allsop, H. Granser, A. J. Millet & I. W. Somerton, “Magnetic interpretation in three dimensions using Euler deconvolution”, Geophysics 55 (1990) 80. https://www.reid-geophys.co.uk

D. T. Thompson, “EULDPTH: A new technique for making computer-assisted depth estimates from magnetic data”, Geophysics 47 (1982) 31. https://www.sciencedirect.com/S1002070508600266.

N. Whitehead & C. Musselman, “Montaj Grav/Mag Interpretation: Processing, Analysis and Visualization Systems for 3D inversion of Potential Field Data for Oasis montajv6.3”, Geosoft Incorporated Canada (2008). https://academicjournals.org/B00067F63907.

D. A. Clarke & D. W. Emerson, “Notes on rock magnetization characteristics in applied geophysical studies”, Exploration Geophysics 22 (1991) 547. https://www.publish.csiro.au/eg/eg991547.

W. M. Telford, L. P. Geldhart & R. E. Sheriff, Applied Geophysics (2nd Edition), Cambridge University Press, Cambridge, 1976, pp. 860. https://kobita1234.files.wordpress.com.

M. Mushayandebvu, P. van Drielz, A. Reid & J. Fairhead, “Magnetic source parameters of two-dimensional structures using extended Euler deconvolution”, Geophysics 66 (2001) 814. https://library.seg.org/doi/abs/10.1190/1.1444971.

P. O. Oluyide, “The Geology of 1:100,000 Sheet 201 (Igabi)”, Geological Survey of Nigeria Report, 1973, pp. 60. https://www.researchgate.net/publication/357031304_16-Article_Text-30-1-10-20211210.

P. McCurry, “Pan African orogeny in Northern Nigeria”, Geol. Sot. Am. Bull. 82 (1971) 3251. https://www.semanticscholar.org/paper.

Application of shifted Vieta-Lucas polynomials for the numerical treatment of Volterra-integro differential equations

Authors

Keywords:

Abstract

REFERENCES

Published

How to Cite

Issue

Section

How to Cite

Latest publications

Information

Make a Submission