Effect of viscous dissipation on steady-state pressure-driven flow in a horizontal porous channel

Authors

  • Deborah Abiola Daramola Department of Mathematics, Airforce Institute of Technology, Kaduna, Nigeria
  • Y. A. Bello Department of Physics, Airforce Institute of Technology, Kaduna, Nigeria
  • Gabriel Samalia Department of Mathematics, Airforce Institute of Technology, Kaduna, Nigeria
  • H. A. Lawal Department of Mathematics, Airforce Institute of Technology, Kaduna, Nigeria
  • Martins Omale Department of Mathematics, Airforce Institute of Technology, Kaduna, Nigeria

Keywords:

Viscous dissipation, Horizontal channel, Pressure gradient

Abstract

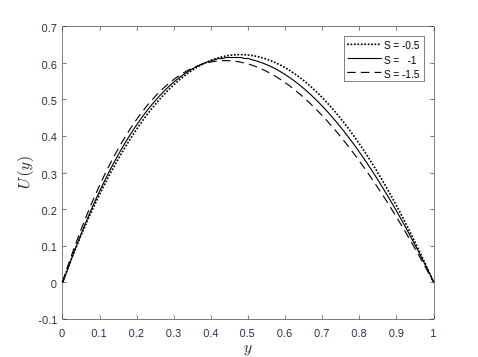
This work considers a pressure-driven flow through a horizontal channel. The flow is considered under the influence of viscous dissipation effect and porosity of the channel plates. The equations governing the flow are solved using the method of undetermined coefficients to obtain a closed-form solution for velocity and temperature of the fluid within the system.  A simulation of the analytical solutions obtained was carried out on MATLAB and the outcome was presented in graphical form. From the investigation, it can be deduced that viscous dissipation acts to increase fluid temperature.

Dimensions

[1] B. Gebhart, ‘‘The influence of viscous dissipation on natural convection’’, J. Fluid Mech. 14 (1962) 265. https://scispace.com/papers/effects-of-viscous-dissipation-on-natural-convection.

[2] E. Zanchini, ‘‘Effect of viscous dissipation on mixed convection in a vertical channel with boundary conditions of the third kind’’, Int. J. Heat and Mass Transfer 41 (1998) 3949. https://doi.org/10.1016/S0017-9310(98)00114-8.

[3] A. Barletta, ‘‘Viscous dissipation effects on laminar mixed convection in a vertical channel’’, Int. J. Heat Mass Transf 41 (1998) 1741. https://doi.org/10.1016/Soo17-9310(98)00074-x.

[4] A. Barletta & E. Zanchini, ‘‘Fully developed laminar mixed convection in an inclined channel with viscous dissipation’’, J. Fluid Mech 433 (2001) 1. https://doi.org/10.10116/S00017-9310(01)00071-0.

[5] M. K. Partha, P. S. V. N. Murthy & G. P. Rajasekhar, ‘‘Effect of viscous dissipation on mixed transfer from an exponentially stretching surface’’, Heat and Mass Trans. 41 (2005) 360. https://doi.org/10.1007/s00231-004-0552-2.

[6] S. Jha, P. Kumar & R. Prasad, ‘‘Effect of viscous dissipation on natural convection flow between vertical parallel plates with time-periodic boundary conditions’’, J. Heat Transfer 134 (2012) 061701. https://doi.org/10.1016/j.cnns.2011.09.020.

[7] A. O. Ajibade & A. M. Umar, ‘‘Effects of viscous dissipation and boundary wall thickness on steady natural convection Couette flow with variable viscosity and thermal conductivity’’, International Journal of Thermofluids 7-8 (2020) 10052. https://doi.org/10.1016/j.ijft.2020.100052.

[8] A. Barletta, M. Celli & P. V. Brandao, ‘‘On mixed convection in horizontal channel, viscous dissipation and flow duality’’, Fluids 7 (2022) 170. https://doi.org/103390/fluids7050170.

[9] A. K. W. Loh, C. G. Mee & B. K. Lim, ‘‘Viscous dissipation effect on forced convective transport of nanofluids in an asymmetrically heated parallel-plate’’, Case Studies in Ther. 35 (2022) 102056. https://doi.org/10.1016/j.csite.2022.102056.

[10] S. Prasad, S. Sood, S.Chandel & D. Sharma ‘‘Impacts of thermal radiation and viscous dissipation on the boundary layer flow of Ferrofluid past a non-flat stretching sheet in a permeable medium: Darcy-Forchheimer’s Model’’, Indian Journal of Science and Technology 17 (2024) 990. https://doi.org/10.17485/IJST/v17i11.3027.

[11] S.M. Hussain, B.S. Goud, P Madheshwaran, ‘‘Effectiveness of nonuniform heat generation (sink) and thermal characterization of a carreau fluid flowing across a nonlinear elongating cylinder: a numerical study’’, ACS Omega 7 (2022) 25309. https://doi.org/10.1021/acsomega.2c02207.

[12] M. H. Shojaefard, A. R. Noorpoor, A. Avanesians & M Ghaffarpour, ‘‘Numerical investigation of flow control by suction and injection on a sub-sonic airfoil’’, American Journal of Applied Sciences 2 (2005) 1474. https://doi.org/10.3844/ajassp.2005.1474.1480.

[13] R. Cortell, ‘‘Suction viscous dissipation and thermal radiation effects on the flow and heat transfer of a power-law fluid past an infinite porous plate’’, Chemical Engineering Research and Design 89 (2011) 85. https://doi.org/10.1016/j.cherd2010.04.017.

[14] I. J. Uwanta & M. M. Hamza, ‘‘Effect of suction/injection on unsteady hydromagnetic convective flow of reactive viscous fluid between vertical porous plates with thermal diffusion’’, Int Sch Res Notices 98 (2014) 1. https://doi.org/10.1155/2014/980270.

[15] H. Upreti, A.K. Pandey & M. Kumar, ‘‘Thermophoresis and suction/injection roles on free convective MHD of Ag-Kerosene oil nanofluid.’’, Journal of Computational Design and Engineering 3 (2020) 386. https://doi.org/10.1093/jcde/qwaa031.

[16] B. X. Wang & X. F. Peng, ‘‘Experimental investigation on liquid forced-convection heat transfer through micro-channels’’, Interrnational Journal of Heat and Mass Transfer 37 (1994) 73. https://doi.org/10.1016/0017-9310(94)90011-6.

[17] D. Wen & Y. Ding, ‘‘Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions’’, International Journal of Heat and Mass Transfer 47 (2004) 5181. https://doi.org/10.1016/j.ijheatmasstransfer.2004.07.012.

[18] A. Raisi, B. Ghasemi & S. Aminossadati, ‘‘A numerical study on the forced convection of laminar nanofluid in a microchannel with both slip and No-Slip conditions’’, Numerical Heat transfer Applications 59 (2011) 540964. https://doi.org/10.1080/10407782.2011.540964.

[19] S. K. Kim, ‘‘Forced convection heat transfer for fully-developed laminar flow of the cross fluid between parallel plates’’, Journal of non-Newtonian fluid mechanics 276 (2020) 104226. https://doi.org/10.1016/j.jnnfm.2019.104226.

[20] X. Sun, S. Li, G. Lin & J. Zhang, ‘‘Effects of flow-induced vibration on forced convection heat transfer two tandem circular cylinders in laminar flow’’, International Journal of Mechanical Sciences 195 (2021) 106238. https://doi.org/10.1016/j.ijmessci.2020.106238.

[21] . P. K. Kundu, I. M. Cohen & D. R. Dowling, ‘‘Laminar Flow’’, in Fluid Mechanics, Fifth (Ed.) Elsevier, Amsterdam, Netherlands, 2012, pp. 309 -359. https://doi.org/10.1016/B978-0-12-382100-3.10008-3.

Published

2025-04-03

How to Cite

Effect of viscous dissipation on steady-state pressure-driven flow in a horizontal porous channel. (2025). Proceedings of the Nigerian Society of Physical Sciences, 2(1), 194. https://doi.org/10.61298/pnspsc.2025.2.194

Issue

Volume 2, NSPS-FUOYE Conference, Feb. 3 - 6, 2025

Section

Articles
Copyright & Licensing

Copyright (c) 2025 Deborah Abiola Daramola, Y. A. Bello, Gabriel Samalia, H. A. Lawal, Martins Omale (Author)

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Effect of viscous dissipation on steady-state pressure-driven flow in a horizontal porous channel. (2025). Proceedings of the Nigerian Society of Physical Sciences, 2(1), 194. https://doi.org/10.61298/pnspsc.2025.2.194