Innovative mathematical application of game theory in solving healthcare allocation problem

Abstract

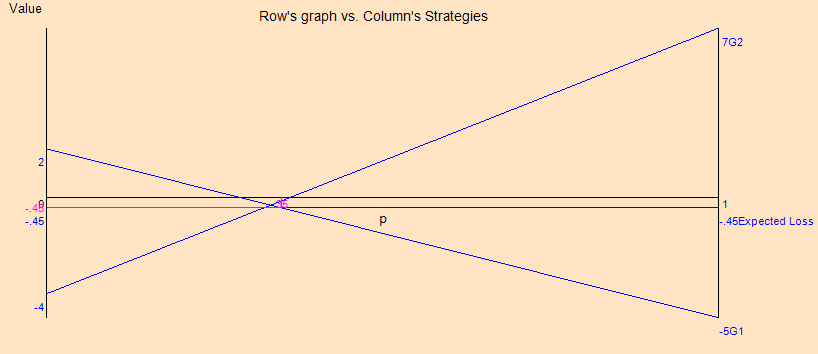
Game theory being a mathematical framework for analyzing strategic interactions among decision makers is increasingly applied to complex problems in healthcare resource allocation. This innovative research strategically applied the game theory model to solve the problem of healthcare allocation. It determined the strategies of Player I (Company A) and Player II (Competitor- Company B), established those strategies using QM (Quality Management) software for Windows, determined the amount of gain or loss experienced by Player I and Player II during the allocations, created various game theory plots, such as the Row’s graph against Column’s strategy and the Column’s graph against Row’s strategies for a pure strategy, and produced various game theory plots, such as the Row’s graph for mixed strategy with given expected loss (%). For it to profit by #1,000,000 (for example) in the case that Company B expands to X location, company A must assign the patients’ bed production plant to location (strategy) D. If Company B introduces the 50% discount or makes #7,000,000, then company A does not have to assign any amount of vaccines manufactured in their firm. The objective is to stop outbreaks in high-risk locations and reduce the spread of infectious diseases. Consequently, a mixed strategy is used, with the aim of maximizing the overall quality of care given to patients while making sure that each facility has the resources necessary for efficient operation.