On the convergence rate of d-dimensional fourth-order beta polynomial kernels
Keywords:
Kernel density estimation, d-dimensional fourth-order kernels, beta polynomial kernels, AMISE, rate of convergenceAbstract
This article focuses on formulating the Asymptotic Mean Integrated Squared Error (AMISE) scheme for d-dimensional fourth-order beta polynomial kernels in the context of kernel density estimation. The primary objective is to assess how this scheme influences the convergence rate, which directly impacts the speed at which the estimated density converges to the true density, contributing to bias reduction. The article employs AMISE as a metric to quantify the overall dissimilarity between the estimated density fˆ and the true density f . Quantitatively, the proposed convergence scheme is compared to existing ones by Deheuvels and Jones et al. across various scenarios of sample sizes and dimensionalities. The study’s findings provide compelling evidence that fourth-order beta polynomial kernels exhibit a significantly faster convergence rate compared to the rates documented in the literature. This accelerated convergence rate implies a substantial improvement in bias reduction capabilities. The results underscore the potential effectiveness of fourth-order beta polynomial kernels as a powerful tool for enhancing the accuracy of kernel density estimation tasks.
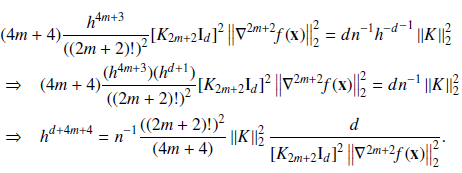
Published
How to Cite
Issue
Section
Copyright (c) 2023 Benson Ade Eniola Afere

This work is licensed under a Creative Commons Attribution 4.0 International License.







