Simulation of optical fiber power amplification via higher-order soliton generation using the extended nonlinear Schrödinger equation
Keywords:
Optical fiber, Soliton, Nonlinear Schrödinger equation, Group velocity dispersion, NonlinearityAbstract
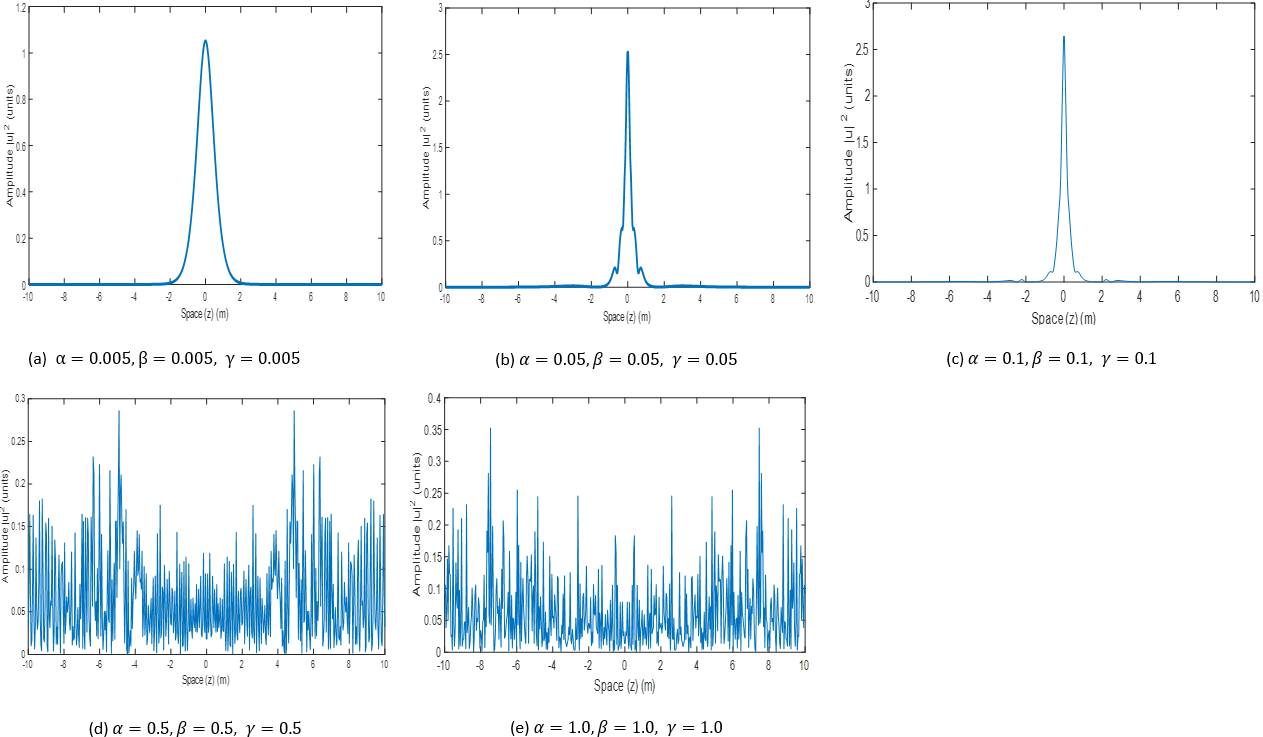
This study seeks to simulate the amplification of the optical fiber power by the generation of higher order solitons. This was achieved by solving an extended form of the nonlinear Schrödinger equation (NLSE) using the split step Fourier method (SSFM) with Gaussian functionals having multiple peaks as initial conditions to simulate the generation of higher order solitons in the optical fiber. Some key fiber parameters such as the coefficients of loss α, group velocity dispersion β and nonlinearity γ were varied and the respective effects on the optical fiber and soliton power were then observed using spatial plots, 3-D contour plots and image color maps. Results obtained showed that in all soliton orders, higher order solitons were created when β was increased from 0.05 to 0.1 fs/nm.km. This shows a broadening of the soliton to create higher order solitons when dispersion is managed within that range which results in a boost in the peak soliton power amplified from 4.5309 W to 14.9508 W and then to 15.0828W as the soliton order was increased from 1st – 2nd – 3rd order respectively using Gaussian functionals. The extra power gained is as a result of the fact that a newly created soliton takes its energy from the radiation present in the dispersed soliton even though the optical power attenuates. It was also observed that, increasing the coefficients α, β and γ from 0.1 – 1.0 results in a continuous attenuation of the optical fiber power leading to the propagation of radiation (noisy signal) in the optical fiber which scatters and exponentially decays after a short distance along the length of the optical fiber.
Published
How to Cite
Issue
Section
Copyright (c) 2025 E. V. Tikyaa, E. S. Nyiyongo , M. B. Ochang, S. D. Igba

This work is licensed under a Creative Commons Attribution 4.0 International License.







