Implicit one-step optimized fourth-derivative hybrid block method for directly solving general third-order IVPs

Authors

  • S. D. Yakubu
    Department of Mathematics, Ibrahim Badamasi Babangida University, Lapai, Nigeria
    School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg 3209, South Africa
    https://orcid.org/0000-0002-4721-2372
  • P. Sibanda
    School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg 3209, South Africa
    https://orcid.org/0000-0003-2115-4642

Keywords:

Fourth-derivative, Optimized hybrid block method, Stiff ODEs

Abstract

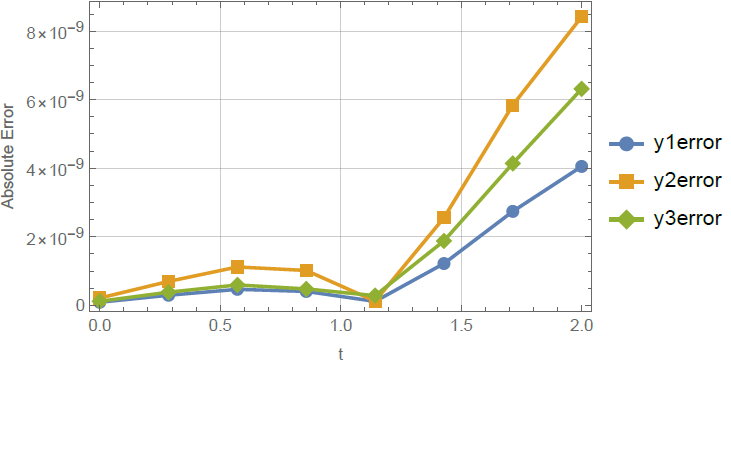
This paper introduces a single-step optimized fourth-derivative block hybrid method specifically designed to solve general third-order initial value problems directly. By incorporating advanced optimization techniques, the method significantly improves accuracy and computational efficiency. Extensive analysis confirms that the method exhibits zero-stability, consistency, A-stability, and convergence properties. Numerical experiments conducted in this study reveal that the proposed method surpasses existing approaches in accuracy, establishing it as a significant advancement in the numerical solution of higher-order initial value problems.

Dimensions

[1] U. Mohammed & R. B. Adeniyi, “A three step implicit hybrid linear multistep method for the solution of third order ordinary differential equations", General Mathematics Notes 25 (2014) 62. http://bit.ly/4lrFHJy

[2] K. O. Lawal, Y. A. Yahaya & S. D. Yakubu, “Four-step block method for solving third order ordinary differential equation", International Journal of Mathematics Trends and Technology 57 (2018) 331.https://doi.org/10.14445/22315373/IJMTT-V57P546. DOI: https://doi.org/10.14445/22315373/IJMTT-V57P546

[3] R. Allogmany & F. Ismail, “Implicit three-point block numerical algorithm for solving third order initial value problem directly with applications", Mathematics 8 (2020) 1771. https://doi.org/10.3390/math8101771. DOI: https://doi.org/10.3390/math8101771

[4] M. A. Adamu, T. Suleman, U. Dahiru & I. A. Aisha, “Continuous implicit one step four-point hybrid block method for the solution of initial value problem for third order ordinary differential equations", International Journal of Science for Global Sustainability 5 (2019) 8. https://tinyurl.com/5688uaud.

[5] M. Alkasassbeh & Z. Omar, “Hybrid one-step block fourth derivative method for the direct solution of third order initial value problems of ordinary differential equations", International Journal of Pure and Applied Mathematics 119 (2018) 207. https://doi.org/10.12732/ijpam.v119i1.17.

[6] M. K. Duromola & A. L. Momoh, “Hybrid numerical method with block extension for direct solution of third order ordinary differential equations", American Journal of Computational Mathematics 9 (2019) 6. https://doi.org/10.4236/ajcm.2019.92006. DOI: https://doi.org/10.4236/ajcm.2019.92006

[7] A. Olagunju & E. Adeyefa, “Hybrid block method for direct integration of first, second and third order IVPs", Cankaya University Journal of Science and Engineering 18 (2021) 1. https://www.academia.edu/103861657/Hybrid_Block_Method_for_Direct_Integration_of_First_Second_and_Third_Order_IVPs.

[8] J. O. Kuboye, O. F. Quadri & O. R. Elusakin, “Solving third order ordinary differential equations directly using hybrid numerical models", Journal of the Nigerian Society of Physical Sciences 2 (2020) 69. https://doi.org/10.46481/jnsps.2020.43. DOI: https://doi.org/10.46481/jnsps.2020.43

[9] M. A. Rufai & H. Ramos, “A variable step-size fourth-derivative hybrid block strategy for integrating third-order IVPs, with applications", International Journal of Computer Mathematics 99 (2022) 292. https://doi.org/10.1080/00207160.2021.1907357. DOI: https://doi.org/10.1080/00207160.2021.1907357

[10] P. Hartman, Ordinary Differential Equations, SIAM, Philadelphia 2002, pp. 1-612. https://epubs.siam.org/doi/10.1137/1.9780898719222. DOI: https://doi.org/10.1137/1.9780898719222

[11] S. D. Yakubu, “Family of one-step A-stable optimized third derivative hybrid block methods for solving general second-order IVPs", AL-Rafidain Journal of Computer Sciences and Mathematics 17 (2023) 125. https://doi.org/10.33899/csmj.2023.143686.1086. DOI: https://doi.org/10.33899/csmj.2023.143686.1086

[12] J. D. Lambert, Numerical methods for ordinary differential systems, Wiley, New York, 1991, pp. 1-304. https://tinyurl.com/36vtbscx

[13] G. G. Dahlquist, “A special stability problem for linear multistep methods", BIT Numerical Mathematics 3 (1963) 27. https://doi.org/10.1007/BF01963532. DOI: https://doi.org/10.1007/BF01963532

[14] Y. D. Jikantoro, F. Ismail, N. Senu & Z. B. Ibrahim, “A new integrator for special third order differential equations with application to thin film flow problem", Indian Journal of Pure and Applied Mathematics 49 (2018) 151. https://doi.org/10.1007/s13226-018-0259-6. DOI: https://doi.org/10.1007/s13226-018-0259-6

[15] R. Genesio & A. Tesi, “Harmonic balance methods for the analysis of chaotic dynamics in nonlinear systems", Automatica 28 (1992) 531. https://doi.org/10.1016/0005-1098(92)90177-H. DOI: https://doi.org/10.1016/0005-1098(92)90177-H

[16] A. L. Osa & O. E. Olaoluwa, “A fifth-fourth continuous block implicit hybrid method for the solution of third order initial value problems in ordinary differential equations", Applied and Computational Mathematics 8 (2019) 50. https://doi.org/10.11648/j.acm.20190803.11. DOI: https://doi.org/10.11648/j.acm.20190803.11

[17] M. Mechee, N. Senu, F. Ismail, B. Nikouravan & Z. Siri, “A three-stage fifth-order Runge-Kutta method for directly solving special third-order differential equation with application to thin film flow problem", Mathematical Problems in Engineering 2013 (2013) 795397. https://doi.org/10.1155/2013/795397. DOI: https://doi.org/10.1155/2013/795397

Published

2025-07-30

How to Cite

Implicit one-step optimized fourth-derivative hybrid block method for directly solving general third-order IVPs. (2025). Recent Advances in Natural Sciences, 3(2), 142. https://doi.org/10.61298/rans.2025.3.2.142

Issue

Volume 3, Issue 2, December 2025 (In Progress)

Section

Articles
Copyright & Licensing

Copyright (c) 2025 S. D. Yakubu, P. Sibanda

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Implicit one-step optimized fourth-derivative hybrid block method for directly solving general third-order IVPs. (2025). Recent Advances in Natural Sciences, 3(2), 142. https://doi.org/10.61298/rans.2025.3.2.142