Zero-inflated and hurdle models with an application to the number of involved axillary lymph nodes in patients with breast cancer in Zimbabwe: A bootstrap resampling validation approach

Abstract

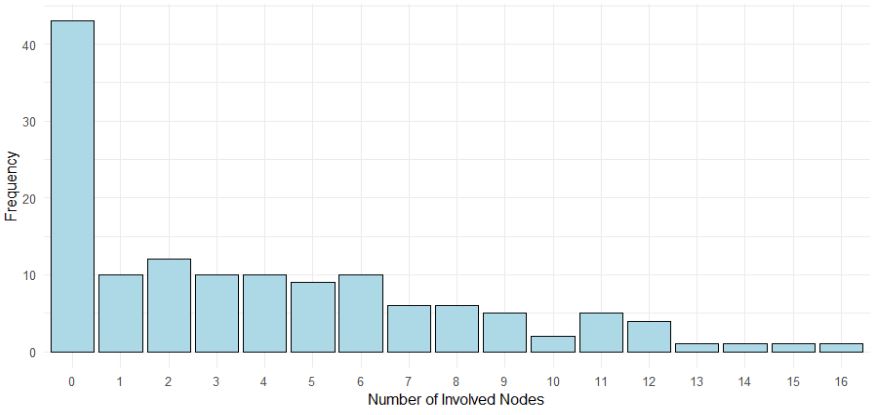
Breast cancer, increasingly prevalent in Zimbabwe, underscores the need to understand the involved axillary nodal status in diagnosed patients for assessment of disease severity and its potential progression. This study was undertaken to investigate factors influencing the number of axillary lymph nodes in breast cancer patients by identifying the best fitting count regression model, validated through bootstrap resampling. A retrospective analysis using hospital-based data for patients diagnosed with breast cancer at one of the two major referral hospitals in Zimbabwe was applied. We evaluated and compared count regression models – Poisson with Negative Binomial (NB), Zero-Inflated Negative Binomial (ZINB), Zero-Inflated Poisson (ZIP), Hurdle Negative Binomial (HNB) and Hurdle Poisson (HP) which are efficient in handling over-dispersed count data to investigate the various risk factors associated with involved axillary lymph nodes. Covariates included age, tumor size, tumor grade, estrogen receptor status, progesterone receptor status and HER2 status. Model diagnostics were assessed using Aikake Information Criterion and Bayesian Information Criterion. The ZINB and HNB models outperformed other models, with the HNB model demonstrating consistency across bootstrap-resampled datasets. Bootstrap resampling validated the reliability of model estimates, addressing biases caused by small sample sizes. Age was significantly associated with the zero-inflation component of the HNB model. This study highlights the importance of selecting appropriate count regression models for analyzing medical data and demonstrates the utility of integrating bootstrap resampling to ensure robust statistical inference. The findings provide actionable insights for therapy planning and resource allocation.