Global convergence properties of a Dai-Liao-type CGM for unconstrained optimization

Oluwaseun Biodun Onuoha

doi:10.61298/rans.2024.2.1.30

Authors

Oluwaseun Biodun Onuoha Department of Mathematical Sciences, Adekunle Ajasin University, P.M.B. 001, Akungba Akoko, Ondo State, Nigeria

Keywords:

Unconstrained optimization, Convergence properties, Descent directions, Objective function

Abstract

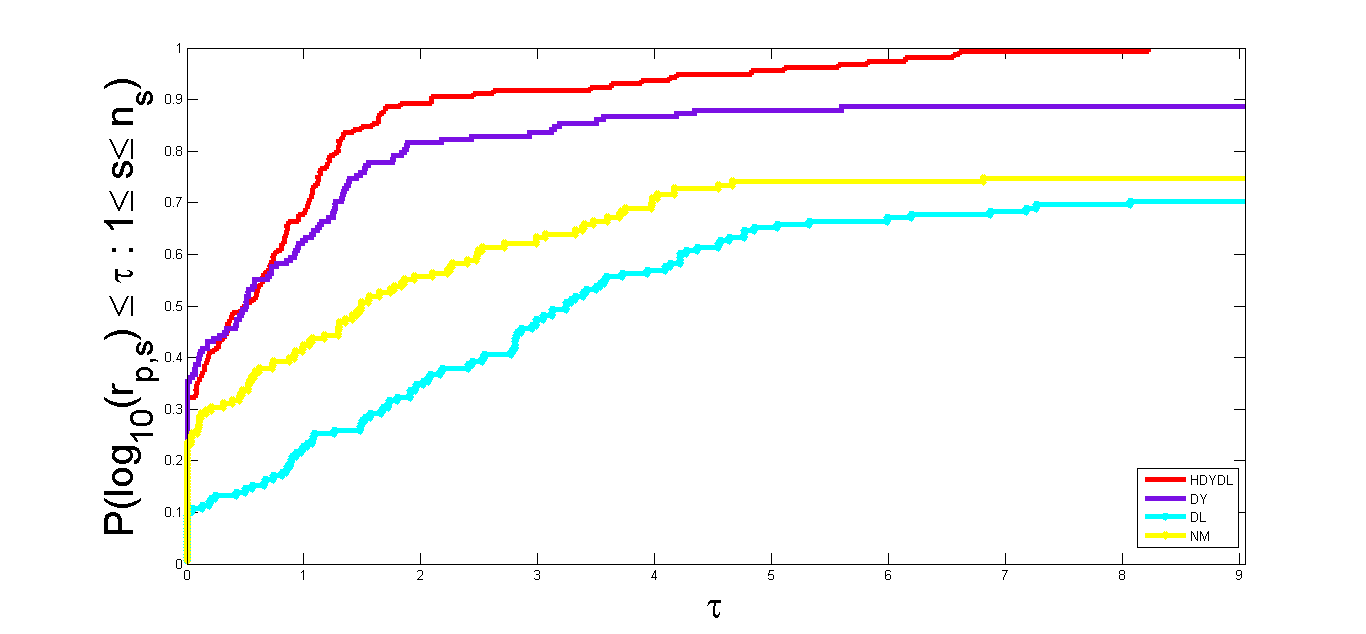
A popular optimization technique called the conjugate gradient method (CGM) is renowned for its effectiveness in addressing problems involving unconstrained optimization. Several conjugate gradient (CG) techniques have been proven to possess global convergence properties both theoretically and numerically. The Dai-Liao-type CGM is a variant that incorporates certain modifications to enhance its convergence properties. This paper examines the global convergence properties of a Dai-Liao-type CGM for unconstrained optimization problems. Theoretically, this study investigates the conditions under which the method ensures convergence to the global minimum of the objective function, focusing on the algorithm’s descent directions, the necessary reduction in objective function values, and termination criteria. A numerical experiment is conducted on a set of unconstrained optimization problems to validate the theoretical results obtained in this work. The numerical findings of this study demonstrate the robustness and reliability of the Dai-Liao-type CGM, showing its ability to find the global optimal solution in a wide range of unconstrained optimization problems.

Dimensions

REFERENCES

E. K. Chong & S. H. Zak, An Introduction to Optimization, Wiley Inter-Science Publication Inc, New York, 2001. https://epdf.tips/an-introduction-to-optimization.html.

O. Olotu, C. Aladesaye & K. A. Dawodu, ‘‘Modified gradient flow method for solving one-dimensional optimal control problem governed by linear equality constraint", Journal of the Nigerian society of Physical Sciences 4 (2022) 146. https://doi.org/10.46481/jnsps.2022.589.

T. T. Yusuf, A. Abidemi, A. S. Afolabi & E. J. Dansu, ‘‘Optimal control of the coronavirus pandemic with impacts on implemented control measures", Journal of the Nigerian Society of Physical Sciences 4 (2022) 88. https://doi.org/10.46481/jnsps.2022.414.

R. Fletcher & C. M. Reeves, ‘‘Function minimization by conjugate gradients", Comput. J. 7 (1964) 149. https://doi.org/10.1093/COMJNL/7.2.149.

M. R. Hestenes & E. Stiefel, ‘‘Methods of conjugate gradients for solving linear systems", J. Res. Natl. Bur. Stand. 49 (1952) 409. https://nvlpubs.nist.gov/nistpubs/jres/049/jresv49n6p409_a1b.pdf.

Y. H. Dai & Y. Yuan, ‘‘A nonlinear conjugate gradient method with a strong global convergence property", SIAM J. Optim. 10 (1999) 177. https://doi.org/10.1137/S1052623497318992.

E. Polak & G. Ribiere, ‘‘Note Sur la Convergence de directions conjugees", ESAIM: Math. Model. Numer. Anal. 3 (1969) 35. https://doi.org/10.1051/M2AN/196903R100351.

B. T. Polyak, ‘‘The conjugate gradient method in extreme problems", Comput. Math. Math. Phys. 9 (1969) 94. https://doi.org/10.1016/0041-5553(69)90035-4.

J. C. Gilbert & J. Nocedal, ‘‘Global convergence properties of conjugate gradient methods for optimization", SIAM Journal on Optimization 2 (1992) 21. https://doi.org/10.1137/0802003.

Z. Wei, S. Yao & L. Liu, ‘‘The convergence properties of some new conjugate gradient methods’’, Applied Mathematics and Computation 183 (2006) 1341. https://doi.org/10.1016/j.amc.2006.05.150.

X. Jiang & J. Jian, ‘‘A sufficient descent Dai-Yuan type nonlinear conjugate gradient method for unconstrained optimization problems", Nonlinear Dyn. 72 (2013) 101. https://doi.org/10.1007/s11071-012-0694-6.

Y. Yueting & C. Mingyuan, ‘‘The global convergence of a new mixed conjugate gradient method for unconstrained optimization", Journal of Applied Mathematics 2012 (2012) 932980. https://doi.org/10.1155/2012/932980.

J. Zhang, Y. Xiao & Z. Wei, ‘‘Nonlinear conjugate gradient methods with sufficient descent condition for large-scale unconstrained optimization", Mathematical Problems in Engineering 2009 (2009) 243290. https://doi.org/10.1155/2009/243290.

S. S. Djordjevic, ‘‘New hybrid conjugate gradient method as a convex combination of HS and FR methods", Journal of Applied Mathematics and Computation 2 (2018) 366. https://doi.org/10.26855/jamc.2018.09.002.

X. Jiang & J. Jian, ‘‘Improved Fletcher-Reeves and Dai-Yuan conjugate gradient methods with strong Wolfe line search", Journal of Computational and Applied Mathematics 348 (2019) 525. https://doi.org/10.1016/j.cam.2018.09.012.

Y. H. Dai & L. Z. Liao, ‘‘New conjugacy conditions and related nonlinear conjugate gradient method", Appl. Math. Optim. 43 (2001) 87. https://doi.org/10.1007/s002450010019.

S. Babaie-Kafaki & R. Ghanbari, ‘‘The Dai-Liao nonlinear conjugate gradient method with optimal parameter choices", Eur. J. Opt. Res. 234 (2014) 625. https://doi.org/10.1016/j.ejor.2013.11.012.

S. Babaie-Kafaki & R. Ghanbari, ‘‘Two adaptive Dai-Liao nonlinear conjugate gradient methods", Iran J. Sci. Technol. Trans. Sci. 42 (2018) 1505. https://doi.org/10.1007/s40995-017-0271-4.

N. Salihu, M. R. Odekunle, A. M. Saleh & S. Salihu, ‘‘A Dai-Liao hybrid Hestenes-Stiefel and Fletcher-Reeves methods for unconstrained optimization", Int. J. Ind. Optim. 2 (2021) 33. https://doi.org/10.12928/IJIO.V2I1. 3054.

M. Lofti & S. M. Hosseini, ‘‘An efficient Dai-Liao type conjugate gradient method by reformulating the CG parameter in the search direction equation", Journal of Computational and Applied Mathematics 371 (2019) 112708. https://doi.org/10.1016/j.cam.2019.112708.

O. B. Akinduko, ‘‘A new conjugate gradient method with sufficient descent property", Earthline J. Math. Sci. 6 (2021) 163. https://doi.org/10.34198/EJMS.6121.163174.

O. B. Onuoha, ‘‘A sufficient descent Dai-Liao type conjugate gradient update parameter", Earthline Journal of Mathematical Sciences 13 (2023) 353. https://doi.org/10.34198/ejms.13223.353368.

A. H. Sheeko & G. M. Al-Naemi, ‘‘Global convergence condition for a new spectra conjugate gradient method for large-scale optimization", J. Phys. Conf. Ser. 1879 (2021) 032001. https://doi.org/10.1088/1742-6596/1879/3/032001.

C. Ahmed & B. Taher, ‘‘Global convergence of new conjugate gradient method with inexact line search", International Journal of Electrical and Computer Engineering 11 (2021) 1469. https://doi.org/10.11591/ijece.v11i2.pp1469-1475.

A. Alhawarat, G. Alhamzi, I. Masmali & Z. Salleh, ‘‘A descent four-term conjugate gradient method with global convergence properties for large-scale unconstrained optimization problems", Mathematical Problems in Engineering 2021 (2021) 6219062. https://doi.org/10.1155/2021/6219062.

P. Wolfe, ‘‘Convergence conditions for ascent methods", SIAM J. Optim. (1969) 226. https://doi.org/10.1137/1011036.

O. O. O. Yousif, M. A. Y. Mohammed, M. A. Saleh & M. K. Elbashir, ‘‘A criterion for the global convergence of conjugate gradient methods under strong Wolfe line search", Journal of King Saud University-Science 34 (2022) 102281. https://doi.org/10.1016/j.jksus.2022.102281.

P. Kaelo, P. Mtagulwa & M. V. Thuto, ‘‘A globally convergent hybrid conjugate gradient method with strong Wolfe conditions for unconstrained optimization", Mathematical Sciences 14 (2020) 1. https://doi.org/10.1007/s40096-019-00310-y.

S. liu & Y. Huang, ‘‘Several guaranteed descent conjugate gradient methods for unconstrained optimization", Journal of Applied Mathematics 2014 (2014) 825958. https://doi.org/10.1155/2014/825958.

O. O. O. Yousif, ‘‘The convergence properties of RMIL+ conjugate gradient method under strong Wolfe line search", Appl. Math. Comp. 367 (2020) 124777. https://doi.org/10.1016/j.amc.2019.124777.

A. Alhawarat, N. T. Trung & Z. Salleh, ‘‘Conjugate gradient method: a developed version to resolve unconstrained optimization problems", Journal of Computer Science 16 (2020) 1220. https://doi.org/10.3844/jcssp.2020.1220.1228.

P. Mtagulwa & P. Kaelo, ‘‘An efficient modified PRP-FR hybrid conjugate gradient method for solving unconstrained optimization problems", Applied Numerical Mathematics 145 (2019) 111. https://doi.org/10.1016/j.apnum.2019.06.003.

J. Nocedal & S. J. Wright, Numerical Optimization, Springer-Verlag Inc., New York, 1999. https://doi.org/10.1007/b98874 .

I. Bongartz, A. R. Conn, N. I. M. Gould & P. L. Toint, ‘‘CUTE: Constrained and unconstrained testing environments", ACM Trans. Math. Softw. 21 (1995) 123. https://doi.org/10.1145/200979.201043.

N. Andrei, ‘‘An unconstrained optimization test functions collection", Adv. Model. Optim. 10 (2008a) 147. https://camo.ici.ro/journal/vol10/v10a10.pdf.

E. D. Dolan & J. J. More, ‘‘Benchmarking optimization software with performance profiles", Math. Program. 91 (2002) 201. https://doi.org/10.1007/s101070100623.

Global convergence properties of a Dai-Liao-type CGM for unconstrained optimization

Authors

Keywords:

Abstract

REFERENCES

Published

How to Cite

Issue

Section

How to Cite

Latest publications

Information

Announcements

Browse

Make a Submission