A novel one-step optimized hybrid block method for solving general second-order ordinary differential equations

Saidu Daudu Yakubu; Precious Sibanda

doi:10.61298/rans.2025.3.1.135

Authors

S. D. Yakubu
[email protected]
School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg 3209, South Africa, Department of Mathematics, Ibrahim Badamasi Babangida University, Lapai, Nigeria
P. Sibanda School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Pietermaritzburg 3209, South Africa https://orcid.org/0000-0003-2115-4642

Keywords:

Collocation, Interpolation, Fourth-derivative, Optimized hybrid block method, Stiff ODEs, Stiff ODEs

Abstract

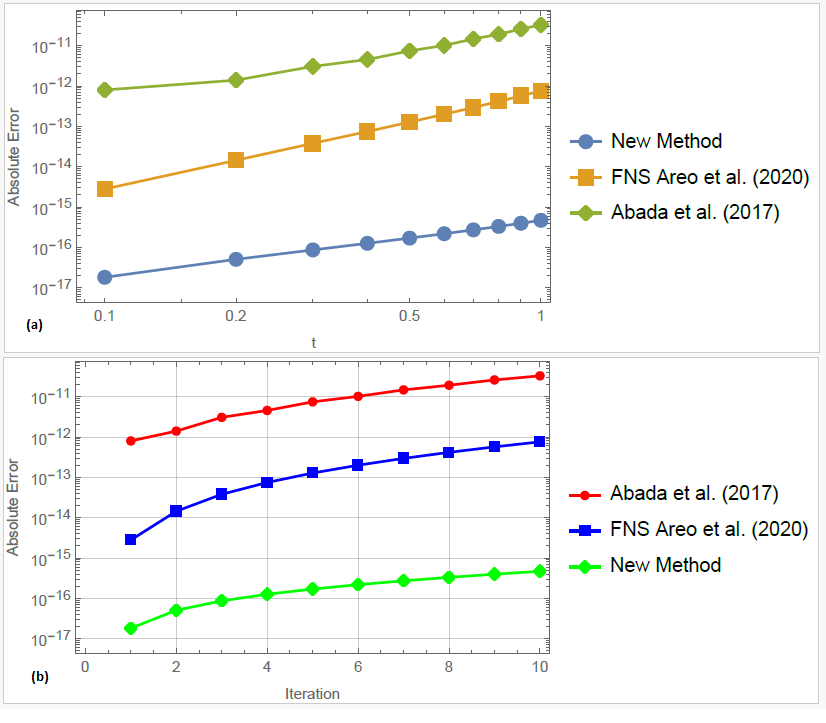
This study introduces a novel one-step hybrid block method for solving both stiff and non-stiff second-order ordinary differential equations (ODEs). The method incorporates optimization techniques and higher derivative functions, addressing the computational challenges of stiff ODEs while ensuring key numerical properties such as zero-stability, A-stability, and convergence. Numerical experiments demonstrate the method’s effectiveness across various problems, including classical examples from heat conduction, electrical circuits, and the Van der Pol oscillator. The results reveal that the proposed method achieves superior accuracy and efficiency, significantly outperforming existing methods in the literature. These findings underscore the potential of this approach as a robust and versatile tool for solving a wide variety of practical ODEs in engineering and applied sciences.

Dimensions

REFERENCES

[1] J. D. Lambert, Computational method in ordinary differential equations, in ‘‘Introductory Mathematics for Scientists and Engineers’’, Wiley, New York, 1973, pp. 1–278. https://doi.org/10.1002/zamm.19740540726.

[2] D. O. Awoyemi, ‘‘A new sixth-order algorithm for general second order ordinary differential equations’’, International J. of Computer Mathematics 77 (2001) 117. https://doi.org/10.1080/00207160108805054.

[3] R. Allogmany, F. Ismailv & Z. B. Ibrahim, ‘‘Implicit two-point block method with third and fourth derivatives for solving general second order ODEs’’, Mathematics and Statistics 7 (2019) 116. https://doi.org/10.13189/ms.2019.070404.

[4] M. A. Rufai & H. Ramos, ‘‘One-step hybrid block method containing third derivatives and improving strategiesfor solving Bratu’s and Troesch’sproblems’’, Numerical Mathematics: Theory, Methods and Appl. 13 (2020) 946. https://doi.org/10.4208/nmtma.oa-2019-0157.

[5] B. T. Olabode & A. L. Momoh, ‘‘Chebyshev hybrid multistep method for directly solving second-order initial and boundary value problems’’, J. of the Nigerian Mathematical Society 39 (2020) 97. https://ojs.ictp.it/jnms/index.php/jnms/article/view/548/106.

[6] O. E. Abolarin, L. S. Akinola, E. O. Adeyefa & B. G. Ogunware, ‘‘Implicit hybrid block methods for solving second, third and fourth orders ordinary differential equations directly’’, Italian J. of Pure and Applied Mathematics 48 (2022) 1. https://ijpam.uniud.it/online_issue/202248/01%20Abolarin-Akinola-Adeyefa-Ogunware.pdf.

[7] Z. Omar & R. Abdelrahim, ‘‘Developing a single step hybrid block method with generalized three off-step points for the direct solution of second-order ordinary differential equations’’, International J. of Mathematical Anal. 9 (2015) 2257. https://doi.org/10.12988/ijma.2015.57181.

[8] S. Qureshi, A. Soomro, E. Hincal, D. Baleanu & A. A. Shaikh, ‘‘An optimized hybrid block method with at least fifth-order Convergence under Fixed and Adaptive Stepsize Formulation’’, Online International Symposium on Applied Mathematics and Engineering (ISAME22) 2022 (2022) 140. https://ntmsci.com/Areas/Conferences/FilesAndImages/19/ISAM-1.pdf.

[9] F. S. Emmanuel & S. Qureshi, ‘‘Convergent numerical method using transcendental function of exponential type to solve continuous dynamical systems’’, Journal of Advanced Physics 7 (2019) 446. https://scholar.google.com/citations?view_op=view_citation&hl=en&user=BAbkMU4AAAAJ&citation_for_view=BAbkMU4AAAAJ:SeFeTyx0c_EC

[10] S. Qureshi, M. A. Akanbi, A. A. Shaikh, A. S. Wusu, O. M. Ogunlaran, W. Mahmoud & M. S. Osman, ‘‘A new adaptive nonlinear numerical method for singular and stiff differential problems’’, Alexandria Engineering Journal 74 (2023) 585. https://doi.org/10.1016/j.aej.2023.05.055.

[11] K. Abuasbeh, S. Qureshi, A. Soomro & M. Awadalla, ‘‘An optimal family of block techniques to solve models of infectious diseases: Fixed and adaptive stepsize strategies’’, Mathematics 11 (2023) 1135. https://doi.org/10.3390/math11051135.

[12] H. Ramos & G. Singh, ‘‘Solving second order two-point boundary value problem accurately by a third derivative hybrid block integrator’’, Applied Maths. and Computation 421 (2022) . https://doi.org/10.1016/j.amc.2022.126960.

[13] R. Singla, G. Singh, V. Kanwar & H. Ramos, ‘‘Efficient adaptive stepsize formulation of an optimized two-step hybrid block method for directly solving second-order initial value problems’’, Computational and Applied Mathematics 40 (2021) 1. https://doi.org/10.1007/540314-021-01599-z.

[14] G. Singh & H. Ramos, ‘‘An optimized two-step hybrid block method formulated in variable step-size mode for integrating y’’ = f(x, y, y’) numerically’’, Numerical Mathematics: Theory, Methods and Applications 12 (2019) 640. https://doi.org/10.4208/nmtma.0a-2018-0036.

[15] B. I. Akinnukawe & S. A. Okunuga, ‘‘One-step block scheme with optimal hybrid points for numerical integration of second-order ordinary differential equations’’, J. of the Nigerian Society of Physical Sciences 6 (2024) 1. https://doi.org/10.46481/jnsps.2024.1827.

[16] P. Hartman, ‘‘Total and Partial Differential Equations'', in Ordinary Differential Equations, SIAM, Philadelphia, 2002, pp. 117--143 . https://epubs.siam.org/doi/book/10.1137/1.9780898719222.

[17] M. Alkasassbeh & Z. Omar, ‘‘Implicit one-step block hybrid third derivative method for the direct solution of initial value problems of second order ordinary differential equations’’, J. of Applied Maths. 2017 (2017) 1. https://doi.org/10.1155/2017/8510948.

[18] A. A. Abada, T. Aboiyar & Y. S. Awari, ‘‘Two-step block hybrid multistep method for the solution of y’’ = f(x, y, y’)’’, Academic J. of Applied Mathematical Sciences 3 (2017) 40. https://ideas.repec.org/a/arp/ajoams/2017p40-45.html.

[19] E. A. Areo, N. O. Adeyanju & S. J. Kayode, ‘‘Direct solution of second order ordinary differential equations using a class of hybrid block methods’’, FUOYE J. of Engineering and Technology 5 (2020) 48. https://doi.org/10.46792/fuoyejet.v5i2.537.

[20] R. Abdelrahim, Z. Omar, O. Ala’yed & B. Batiha, ‘‘Hybrid third derivative block method for the solution of general second order initial value problems with general one-step point’’, European J. of Pure and Applied Maths. 12 (2019) 1199. https://doi.org/10.29020/nybg.ejpam.v12i3.3425.

[21] S. N. Jator & J. Li, ‘‘A self-starting linear multistep method for a direct solution of the general second-order initial value problems’’, International J. of Computer Maths. 86 (2009) 827. https://doi.org/10.1080/00207160701708250.

[22] E. O. Omole & B. G. Ogunware, ‘‘3-point single hybrid block method (3pshbm) for direct solution of general second order initial value problems of ordinary differential equations’’, J. of Scientific Research and Reports 20 (2018) 1. https://doi.org/10.9734/JSRR/2018/19862.

[23] F. O. Obarhua, ‘‘An efficient two-step symmetric hybrid block method for solving second order initial value problems of ordinary differential equations’’, International J. of Research and Scientific Innovation 6 (2019) 200. https://www.researchgate.net/profile/Friday-Obarhua.

[24] Y. A. Yahaya & A. M. Saqir, ‘‘An order five implicit 3-step block method for solving ordinary differential equations’’, The Pacific J. of Science and Technology 14 (2013) 176. https://www.researchgate.net/publication/322623141_An_Order_Five_Implicit_3_-_Step_Block_Method_for_Solving_Ordinary_Differential_Equations.

[25] J. Guckenheimer & P. Holmes, ‘‘Differential equation and dynamic system’’, in Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer-Verlag, New York, 1983, pp. 2–65. https://link.springer.com/book/10.1007/978-1-4612-1140-2.